Condition Number

A condition number measures how sensitive is the solution of equation(s) to perturbations in the input is.

Introduction

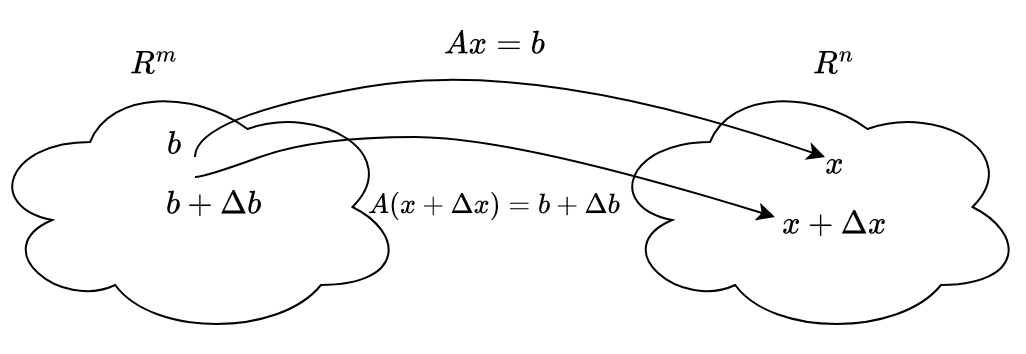
Consider a system of linear equations in the form of \(Ax=b\), where we are interested to find \(x\). So we have a solution space of \(x \in R^{n}\) for \(b \in R^{m}\) while unchanging \(A\).

Now our objective is to quantify the change in solution space of \(x\) if we add some perturbations or error term to input space of \(b\). As we can see in the above figure that altering the input space will give us $$A(x+\Delta{x})=b+\Delta{b}$$

Te reach our objective, we first need to understand what are matrix norms.

Matrix Norms

The norm of square matrix \(A\) is non-negative real number denoted \(\lVert A \rVert\). It is a way of determining the “size” of a matrix that is not necessarily related to how many rows or columns the matrix has. There are various different ways of defining a matrix norm.

1-Norm

$$\lVert A \rVert_{1} = \max_{1 \le \ j \ \le n}(\sum_{i=1}^{n}|a_{ij}|)$$

We sum the absolute values down each column and then take the max value out of those.

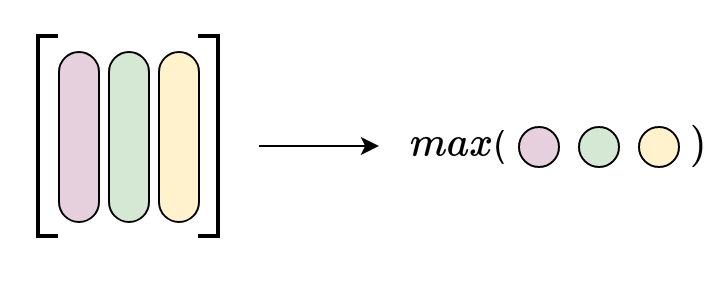
Infinity-Norm

$$\lVert A \rVert_{\infty} = \max_{1 \le \ i \ \le n}(\sum_{j=1}^{n}|a_{ij}|)$$

We sum the absolute values along each row and then take the max out of those.

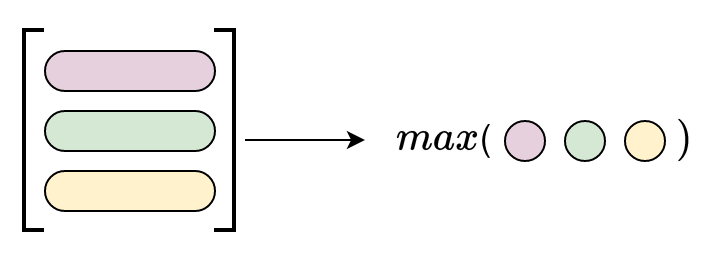
We have taken square matrix \(A\) but same formulas can be applied for rectangular matrices too.

Properties

  1. \(\lVert A \rVert\) \(\ge\) 0 for any square matrix
  2. \(\lVert A \rVert\) \(=\) 0 iff \(A=0\)
  3. \(\lVert kA \rVert\) = |k|\(\lVert A \rVert\), for any scalar \(k\)
  4. \(\lVert A + B \rVert \le \lVert A \rVert + \lVert B \rVert\)
  5. \(\lVert AB \rVert \le \lVert A \rVert \lVert B \rVert\)

Condition Number

Matrix norm is enough for us to start working on condition number. We will start by accounting in \(Ax=b\) and \(A(x+\Delta{x})=b+\Delta{b}\).

$$ \begin{aligned} \cancel{Ax} &= \cancel{b} \cr \cancel{Ax}+A\Delta{x} &= \cancel{b} + \Delta{b} \cr \hline \cr A\Delta{x} &= \Delta{b} \cr \hline \end{aligned} $$

applying the \(5^{th}\) property of matrix norms to \(Ax=b\)

$$ \begin{aligned} \lVert b \rVert = \lVert Ax \rVert &\le \lVert A \rVert \lVert x \rVert \cr \frac{1}{\lVert x \rVert} &\le \frac{\lVert A \rVert}{\lVert b \rVert} \end{aligned} $$

multiplying \(A\Delta{x} = \Delta{b}\) by \(A^{-1}\) on both sides

$$ \begin{aligned} A^{-1}A\Delta{x} &= A^{-1}\Delta{b} \cr I\Delta{x} &= A^{-1}\Delta{b} \end{aligned} $$ taking matrix norm on both sides $$\lVert \Delta{x} \rVert = \lVert A^{-1}\Delta{b} \rVert \le \lVert A^{-1} \rVert \lVert \Delta{b} \rVert$$

we get, $$\boxed{\frac{\lVert \Delta{x} \rVert}{\lVert x \rVert} \le \lVert A \rVert \lVert A^{-1} \rVert \frac{\lVert \Delta{b} \rVert}{\lVert b \rVert}}$$ This says that the upper bound in relative error of \(x\) would be scaled to \(\kappa(A) = \lVert A \rVert \lVert A^{-1} \rVert\) multiplied by relative error in \(b\), where \(\kappa(A)\) is Condition Number. Calculating \(\lVert A \rVert\) is relatively easy than finding \(\lVert A^{-1} \rVert\).

\(\Delta{b}\) is usually generated by rounding error programs, or when we made some approximation mistake. Hence, it is quite small and this implies relative error in \(x\) depends on condition number. Also we generally use infinity-norm to find matrix norms of matrices.

Example
Consider 5x1+7x2=0.75x_{1} + 7x_{2} = 0.7, 7x1+10x2=17x_{1} + 10x_{2} = 1

Solution x = [0, 0.1]

Perturbed system 5x1+7x2=0.695x_{1} + 7x_{2} = 0.69, 7x1+10x2=1.017x_{1} + 10x_{2} = 1.01
has the solution x’ = [-0.17, 0.22]

The relative error in the xx is given by, ∥Δx∥∥x∥=1.7\frac{\lVert \Delta{x} \rVert}{\lVert x \rVert} = 1.7

and the relative error in bb is given by, ∥Δb∥∥b∥=0.01\frac{\lVert \Delta{b} \rVert}{\lVert b \rVert} = 0.01

now 1% error in input is giving a 170% error in output which is significantly large.

Let’s check the condition number using the infinity norm. κ(A)=289\kappa(A) = 289

This says that the upper bound of relative error in solution space is 289x0.01=2.89289x0.01=2.89

A matrix with large condition number is said to be ill conditioned. Whereas a matrix with small condition matrix is said to be well conditioned. Although large and small is hard to quantify since it depends on many factors of which some can be how powerful computing power we working with, what type of applications we are working with etc.

Theoram
Let AA be a square non-singular matrix then for any singular matrix of the same size BB, we have 1κ(A)≤∥A−B∥∥A∥\frac{1}{\kappa(A)} \le \frac{\lVert A - B\rVert}{\lVert A \rVert}

This shows that if you have singular matrix which is quite close to non-singular matrix then it will decrease the relative error but inversely decrease the condition number too. In other words, closer the singular matrix to non-singular matrix higher the condition number.

Example
Consider a matrix B=(1111)B=\begin{pmatrix} 1 & 1 \\ 1 & 1 \end{pmatrix} which is singularly non-invertible since its determinant is 0.
For any ϵ>0\epsilon \gt 0, let A=(11+ϵ1−ϵ1)A=\begin{pmatrix} 1 & 1+\epsilon \\ 1-\epsilon & 1 \end{pmatrix} then, A−1=ϵ−2(1−1−ϵ−1+ϵ1)A^{-1} = \epsilon^{-2}\begin{pmatrix} 1 & -1-\epsilon \\ -1 + \epsilon & 1 \end{pmatrix} Taking matrix norms,
∥A∥∞=2+ϵ\lVert A \rVert_{\infty} = 2+\epsilon and ∥A−1∥∞=ϵ−2(2+ϵ)\lVert A^{-1} \rVert_{\infty} = \epsilon^{-2}(2+\epsilon)
then, κ(A)=∥A∥∞∥A−1∥∞=(2ϵ+1)2>4ϵ2\kappa(A)=\lVert A \rVert_{\infty}\lVert A^{-1} \rVert_{\infty}= (\frac{2}{\epsilon} + 1)^{2} > \frac{4}{\epsilon^{2}} let ϵ≤0.01⟹κ(A)=40,000\epsilon \le 0.01 \implies \kappa(A)=40,000
As ϵ→0,A→B\epsilon \rightarrow 0, A \rightarrow B and κ(A)→∞\kappa(A) \rightarrow \infty. This will result in very sensitive computation since κ(A)→∞\kappa(A) \rightarrow \infty

References

[1] Matrix norms 30 - Imperial College London

[2] Prof. S. Baskar, “Week 3 : Lecture 16 : Matrix Norms: Condition Number of a Matrix.”, YouTube, uploaded by IIT Bombay July 2018, 02 February 2023, https://www.youtube.com/watch?v=IXNz7BU0CDc

[3] Robert van de Geijn, “1 4 1 The condition number of a matrix”, YouTube, uploaded by Advanced LAFF, 17 September 2019, https://www.youtube.com/watch?v=CGfXxLnnHtg&t=379s

[4] Jones, A. (2020, May 17). Condition numbers. Andy Jones. Retrieved April 15, 2023, from https://andrewcharlesjones.github.io/journal/condition-number.html